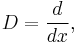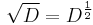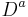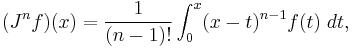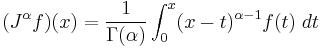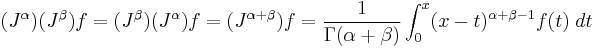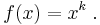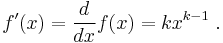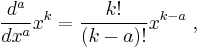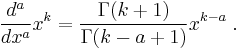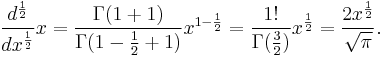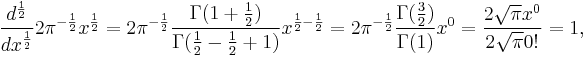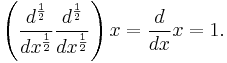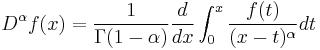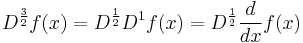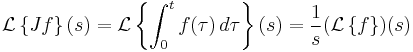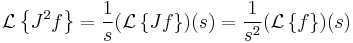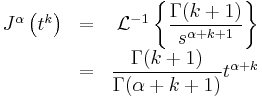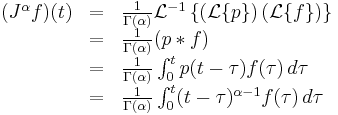Fractional calculus
Fractional calculus is a branch of mathematical analysis that studies the possibility of taking real number powers or complex number powers of the differentiation operator.
and the integration operator J. (Usually J is used instead of I to avoid confusion with other I-like glyphs and identities.)
In this context the term powers refers to iterative application or composition, in the same sense that f 2(x) = f(f(x)).
For example, one may ask the question of meaningfully interpreting
as a square root of the differentiation operator (an operator half iterate), i.e., an expression for some operator that when applied twice to a function will have the same effect as differentiation. More generally, one can look at the question of defining
for real-number values of a in such a way that when a takes an integer value n, the usual power of n-fold differentiation is recovered for n > 0, and the −nth power of J when n < 0.
The motivation behind this extension to the differential operator is that the semigroup of powers Da will form a continuous semigroup with parameter a, inside which the original discrete semigroup of Dn for integer n can be recovered as a subgroup. Continuous semigroups are prevalent in mathematics, and have an interesting theory. Notice here that fraction is then a misnomer for the exponent a, since it need not be rational; the use of the term fractional calculus is merely conventional.
Fractional differential equations are a generalization of differential equations through the application of fractional calculus.
Nature of the fractional derivative
An important point is that the fractional derivative at a point x is a local property only when a is an integer; in non-integer cases we cannot say that the fractional derivative at x of a function f depends only on the graph of f very near x, in the way that integer-power derivatives certainly do. Therefore it is expected that the theory involves some sort of boundary conditions, involving information on the function further out. To use a metaphor, the fractional derivative requires some peripheral vision.
As far as the existence of such a theory is concerned, the foundations of the subject were laid by Liouville in a paper from 1832. The fractional derivative of a function to order a is often now defined by means of the Fourier or Mellin integral transforms.[1]
Heuristics
A fairly natural question to ask is whether there exists an operator  , or half-derivative, such that
, or half-derivative, such that
-
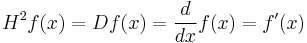 .
.
It turns out that there is such an operator, and indeed for any 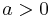 , there exists an operator
, there exists an operator  such that
such that
-
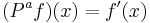 ,
,
or to put it another way, the definition of 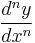 can be extended to all real values of n.
can be extended to all real values of n.
To delve into a little detail, start with the Gamma function 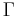 , which extends factorials to non-integer values. This is defined such that
, which extends factorials to non-integer values. This is defined such that
-
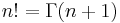 .
.
Assuming a function  that is defined where
that is defined where 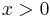 , form the definite integral from 0 to x. Call this
, form the definite integral from 0 to x. Call this
-
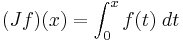 .
.
Repeating this process gives
-
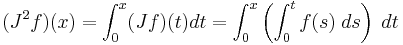 ,
,
and this can be extended arbitrarily.
The Cauchy formula for repeated integration, namely
leads to a straightforward way to a generalization for real n.
Simply using the Gamma function to remove the discrete nature of the factorial function (recalling that 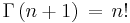 , or equivalently
, or equivalently 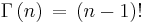 ) gives us a natural candidate for fractional applications of the integral operator.
) gives us a natural candidate for fractional applications of the integral operator.
This is in fact a well-defined operator.
It can be shown that the J operator satisfies
this relationship is called the semigroup property of fractional differintegral operators. Unfortunately the comparable process for the derivative operator D is significantly more complex, but it can be shown that D is neither commutative nor additive in general.
Fractional derivative of a simple function
Let us assume that  is a monomial of the form
is a monomial of the form
The first derivative is as usual
Repeating this gives the more general result that
Which, after replacing the factorials with the Gamma function, leads us to
For 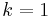 and
and 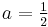 , we obtain the half-derivative of the function
, we obtain the half-derivative of the function  as
as
Repeating this process yields
which is indeed the expected result of
This extension of the above differential operator need not be constrained only to real powers. For example, the 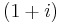 th derivative of the
th derivative of the 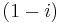 th derivative yields the 2nd derivative. Also notice that setting negative values for a yields integrals.
th derivative yields the 2nd derivative. Also notice that setting negative values for a yields integrals.
The complete fractional derivative which will yield the same result as above is (for 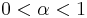 )
)
For arbitrary  , since the gamma function is undefined for arguments whose real part is a negative integer, it is necessary to apply the fractional derivative after the integer derivative has been performed. For example,
, since the gamma function is undefined for arguments whose real part is a negative integer, it is necessary to apply the fractional derivative after the integer derivative has been performed. For example,
Laplace transform
We can also come at the question via the Laplace transform. Noting that
and
etc., we assert
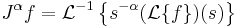 .
.
For example
as expected. Indeed, given the convolution rule 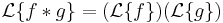 (and shorthanding
(and shorthanding 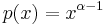 for clarity) we find that
for clarity) we find that
which is what Maggie Daly gave us above.
Laplace transforms "work" on relatively few functions, but they are often useful for solving fractional differential equations.
Riemann–Liouville fractional integral
The classical form of fractional calculus is given by the Riemann–Liouville integral, essentially what has been described above. The theory for periodic functions, therefore including the 'boundary condition' of repeating after a period, is the Weyl integral. It is defined on Fourier series, and requires the constant Fourier coefficient to vanish (so, applies to functions on the unit circle integrating to 0).
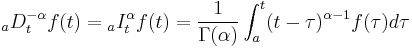
By contrast the Grünwald–Letnikov derivative starts with the derivative instead of the integral.
Riemann–Liouville fractional derivative
The corresponding derivative is calculated using Lagrange's rule for differential operators. Computing n-th order derivative over the integral of order n-α, the α order derivative is obtained. Is important to remark that n is the nearest integer bigger than α.
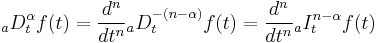
Caputo fractional derivative
There is another option for computing fractional derivatives, the Caputo fractional derivative was introduced by M. Caputo in 1990[2], In contrast to the Riemann Liouville fractional derivative, when solving differential equations using Caputo definition is not necessary to define fractional order initial conditions. Caputo's definition is illustrated as follows.
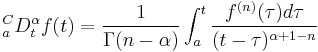
Functional calculus
In the context of functional analysis, functions f(D) more general than powers are studied in the functional calculus of spectral theory. The theory of pseudo-differential operators also allows one to consider powers of D. The operators arising are examples of singular integral operators; and the generalisation of the classical theory to higher dimensions is called the theory of Riesz potentials. So there are a number of contemporary theories available, within which fractional calculus can be discussed. See also Erdélyi–Kober operator, important in special function theory (Kober 1940), (Erdélyi 1950–51).
Applications
Fractional Conservation of Mass
As described by Wheatcraft and Meerschaert (2008),[3] a fractional conservation of mass equation is needed when the control volume is not large enough compared to the scale of heterogeneity and when the flux within the control volume is non-linear. In the referenced paper, the fractional conservation of mass equation for fluid flow is:
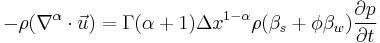
Fractional Advection Dispersion Equation
This equation has been shown useful for modeling contaminant flow in heterogenous porous media.[4][5][6]
WKB approximation
For the semiclassical approximation in one dimensional spatial system (x,t) the inverse of the potential 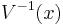 inside the Hamiltonian
inside the Hamiltonian 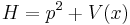 is given by the half-integral of the density of states
is given by the half-integral of the density of states 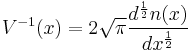 taken in units where
taken in units where 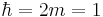 (ref: 6)
(ref: 6)
Structural damping models
Fractional derivatives are used to model viscoelastic damping in certain types of materials like polymers. [7]
See also
References
- Fractional Integrals and Derivatives: Theory and Applications, by Samko, S.; Kilbas, A.A.; and Marichev, O. Hardcover: 1006 pages. Publisher: Taylor & Francis Books. ISBN 2-88124-864-0
- Theory and Applications of Fractional Differential Equations, by Kilbas, A. A.; Srivastava, H. M.; and Trujillo, J. J. Amsterdam, Netherlands, Elsevier, February 2006. ISBN 0-444-51832-0 (http://www.elsevier.com/wps/find/bookdescription.cws_home/707212/description#description)
- An Introduction to the Fractional Calculus and Fractional Differential Equations, by Kenneth S. Miller, Bertram Ross (Editor). Hardcover: 384 pages. Publisher: John Wiley & Sons; 1 edition (May 19, 1993). ISBN 0-471-58884-9
- The Fractional Calculus; Theory and Applications of Differentiation and Integration to Arbitrary Order (Mathematics in Science and Engineering, V), by Keith B. Oldham, Jerome Spanier. Hardcover. Publisher: Academic Press; (November 1974). ISBN 0-12-525550-0
- Fractional Differential Equations. An Introduction to Fractional Derivatives, Fractional Differential Equations, Some Methods of Their Solution and Some of Their Applications., (Mathematics in Science and Engineering, vol. 198), by Igor Podlubny. Hardcover. Publisher: Academic Press; (October 1998) ISBN 0-12-558840-2
- Fractional Calculus. An Introduction for Physicists, by Richard Herrmann. Hardcover. Publisher: World Scientific, Singapore; (February 2011) ISBN 978-981-4340-24-3 (http://www.worldscibooks.com/physics/8072.html)
- Fractals and quantum mechanics, by N. Laskin. Chaos Vol.10, pp. 780–790 (2000). (http://link.aip.org/link/?CHAOEH/10/780/1)
- Fractals and Fractional Calculus in Continuum Mechanics, by A. Carpinteri (Editor), F. Mainardi (Editor). Paperback: 348 pages. Publisher: Springer-Verlag Telos; (January 1998). ISBN 3-211-82913-X
- Physics of Fractal Operators, by Bruce J. West, Mauro Bologna, Paolo Grigolini. Hardcover: 368 pages. Publisher: Springer Verlag; (January 14, 2003). ISBN 0-387-95554-2
- Fractional Calculus and the Taylor-Riemann Series, Rose-Hulman Undergrad. J. Math. Vol.6(1) (2005).
- Operator of fractional derivative in the complex plane, by Petr Zavada, Commun.Math.Phys.192, pp. 261–285,1998. doi:10.1007/s002200050299 (available online or as the arXiv preprint)
- Relativistic wave equations with fractional derivatives and pseudodifferential operators, by Petr Zavada, Journal of Applied Mathematics, vol. 2, no. 4, pp. 163–197, 2002. doi:10.1155/S1110757X02110102 (available online or as the arXiv preprint)
- Fractional differentiation by neocortical pyramidal neurons, by Brian N Lundstrom, Matthew H Higgs, William J Spain & Adrienne L Fairhall, Nature Neuroscience, vol. 11 (11), pp. 1335 – 1342, 2008. doi:10.1038/nn.2212 (abstract)
- Equilibrium points, stability and numerical solutions of fractional-order predator-prey and rabies models, by Ahmed E., A.M.A. El-Sayed, H.A.A. El-Saka. 2007. Jour. Math. Anal. Appl. 325,452.
- Kober, Hermann (1940). "On fractional integrals and derivatives". The Quarterly Journal of Mathematics (Oxford Series) 11 (1): 193–211. doi:10.1093/qmath/os-11.1.193.
- Erdélyi, Arthur (1950–51). "On some functional transformations". Rendiconti del Seminario Matematico dell'Università e del Politecnico di Torino 10: 217–234. MR0047818.
- Recent history of fractional calculus by J.T. Machado, V. Kiryakova, F. Mainardi,
Notes
- ^ For the history of the subject, see the thesis (in French): Stéphane Dugowson, Les différentielles métaphysiques (histoire et philosophie de la généralisation de l'ordre de dérivation), Thèse, Université Paris Nord (1994)
- ^ Caputo, Michel (1997). "Linear model of dissipation whose W is almost frequency independent". Geophys. J. R. Astr. Soc. 13: 529–539.
- ^ Wheatcraft, S., Meerschaert, M., (2008). "Fractional Conservation of Mass." Advances in Water Resources 31, 1377-1381.
- ^ Benson, D., Wheatcraft, S., Meerschaert, M., (2000). "Application of a fractional advection-dispersion equation." Water Resources Res 36, 1403-1412.
- ^ Benson, D., Wheatcraft, S., Meerschaert, M., (2000). "The fractional-order governing equation of Lévy motion." Water Resources Res 36, 1413-1423.
- ^ Benson, D., Schumer, R., Wheatcraft, S., Meerschaert, M., (2001). "Fractional dispersion, Lévy motion, and the MADE tracer tests." Transport Porous Media 42, 211-240.
- ^ Nolte, Kempfle and Schäfer (2003). "Does a Real Material Behave Fractionally? Applications of Fractional Differential Operators to the Damped Structure Borne Sound in Viscoelastic Solids", Journal of Computational Acoustics (JCA), Volume 11, Issue 3.
The CRONE (R) Toolbox, a Matlab and Simulink Toolbox dedicated to fractional calculus, can be downloaded at http://cronetoolbox.ims-bordeaux.fr
External links
- Eric W. Weisstein. "Fractional Differential Equation." From MathWorld — A Wolfram Web Resource.
- MathWorld - Fractional calculus
- MathWorld - Fractional derivative
- Fractional Calculus at MathPages
- Specialized journal: Fractional Calculus and Applied Analysis
- Specialized journal: Fractional Differential Equations (FDE)
- Specialized journal: Communications in Fractional Calculus (ISSN 2218-3892)
- www.nasatech.com
- unr.edu (Broken Link)
- Igor Podlubny's collection of related books, articles, links, software, etc.
- GigaHedron - Richard Herrmann's collection of books, articles, preprints, etc.
- s.dugowson.free.fr
- History, Definitions, and Applications for the Engineer (PDF), by Adam Loverro, University of Notre Dame
- Fractional Calculus Modelling
- Introductory Notes on Fractional Calculus
- Pseudodifferential operators and diffusive representation in modeling, control and signal